Persamaan dan Pertidaksamaan Nilai Mutlak Linear Satu Variabel
Dari sudut pandang geometri, nilai mutlak dari x ditulis | x |, adalah jarak dari x ke 0 pada garis bilangan real. Karena jarak selalu positif atau nol maka nilai mutlak x juga selalu bernilai positif atau nol untuk setiap x bilangan real.
| x | = -x jika x ≥ 0
| x | = -x jika x < 0
Definisi diatas dapat kita maknai sebagai berikut :
Nilai mutlak bilangan positif atau nol adalah bilangan itu sendiri dan nilai mutlak bilangan negatif adalah lawan dari bilangan tersebut.
Sebagai contoh,
| 7 | = 7 | 0 | = 0 | -4 | = -(-4) = 4
Jadi, jelas bahwa nilai mutlak setiap bilangan real akan selalu bernilai positif atau nol.
Persamaan hanya bernilai benar jika x ≥ 0. Untuk x < 0, maka . Dapat kita tulis Jika kita perhatikan, bentuk diatas sama persis dengan definisi nilai mutlak x. Oleh karenanya, pernyataan berikut benar untuk setiap x bilangan real. Jika kedua ruas persamaan diatas kita kuadratkan akan diperoleh Persamaan terakhir ini merupakan konsep dasar penyelesaian persamaan atau pertidaksamaan nilai mutlak dengan cara menguadratkan kedua ruas. Seperti yang kita lihat, tanda mutlak bisa hilang jika dikuadratkan.
Namun, pada artikel ini kita akan lebih fokus pada bentuk linier, baik dari kasus ataupun solusi, tanpa melibatkan bentuk kuadrat.
Menyelesaikan Persamaan dan Pertidaksamaan Nilai Mutlak
Menyelesaikan Persamaan Mutlak
Nilai mutlak suatu bilangan dapat diartikan jarak antara bilangan tersebut dari titik nol(0). Dengan demikian jarak selalu bernilai positif.
Misalnya:
Parhatikan garis bilangan berikut.
Jarak angka 6 dari titik 0 adalah 6
Jarak angka -6 dari titik 0 adalah 6
jarak angka -3 dari titik 0 adalah 3
Jarak angka 3 dari titik0 adalah 3.
Dari penjelesan di atas memang tampak bahwa nilai mutlak suatu bilangan selalu bernilai positif.
Berkaitan dengan menentukan nilai mutlak suatu bilangan, maka muncullah tanda mutlak. Tanda mutlak disimbolkan dengan garis 2 ditepi suatu bilangan atau bentuk aljabar.
Misalnya seperti berikut.
Secara umum, bentuk persamaan nilai mutlak dapat dimaknai seperti berikut.
Jika kita mempunyai persamaan dalam bentuk aljabar, maka dapat dimaknai sebagai berikut.
Jadi, bentuk dasar di atas dpat digunakan untuk membantu menyelesaikan persamaan mutlak.
Lebih jelasnya perhatikan contoh-contoh berikut.
Contoh
Tentukan himpunan penyelesaian dari persamaan nilai Mutlak di bawah ini.
Jawaban:
Bentuk-Bentuk persamaan nilai mutlak di atas dapat diselesaikan sebagai berikut. Pada prinsipnya, langkah langkah penyelesaian nilai mutlak diusahakan bentuk mutlak berada di ruas kiri.
1. Pada bentuk ini ada dua penyelesaian.
(*) x + 5 = 3 , maka x = 3 - 5 = -2
(**) x + 5 = -3, maka x = -3 - 5 = -8
Jadi, himpunan penyelesaiannya adalah {-2, -8}
2. Pada bentuk ini ada dua penyelesaian.
(*) 2x + 3 = 5 , maka 2x = 5 - 3
2x = 2 <==> x = 1
(**) 2x + 3 = -5 , maka 2x = -5 -3
2x = -8 <==> x = -4
Jadi, himpunan penyelesaiannya adalah {-4, 1}
3. Perhatikan bentuk aljabar di dalam tanda mutlak, yaitu x+1. Penyelesaian persamaan nilai mutlak ini juga dibagi menjadi dua bagian.
Bagian pertama untuk batasan x+1>= 0 atau x >= -1
Bagian kedua untuk batasan x+1< 0 atau x < -1
Mari kita selesaikan.
(*) untuk x >=-1
Persamaan mutlak dapat ditulis:
(x + 1) + 2x = 7
3x = 7 - 1
3x = 6
x = 2 (terpenuhi, karena batasan >= -1)
(**) untuk x < -1
Persamaan mutlak dapat ditulis:
-(x + 1) + 2x = 7
-x - 1 + 2x = 7
x = 7 + 1
x = 8 (tidak terpenuhi, karena batasan < -1)
Jadi, Himpunan penyelesaiannya adalah {2}.
4.
Perhatikan bentuk aljabar di dalam tanda mutlak, yaitu 3x + 4. Penyelesaian persamaan nilai mutlak ini juga dibagi menjadi dua bagian.
Bagian pertama untuk batasan 3x+4>= 0 atau x >= -4/3
Bagian kedua untuk batasan 3x+4< 0 atau x < -4/3
Mari kita selesaikan.
(*) untuk x >=-4/3
Persamaan mutlak dapat ditulis:
(3x + 4) = x - 8
3x - x = -8 - 4
2x =-12
x = -6 (tidak terpenuhi, karena batasan >= -4/3)
(**) untuk x < -4/3
Persamaan mutlak dapat ditulis:
-(3x + 4) = x - 8
-3x - 4 = x -8
-3x - x = -8 + 4
-4x = -4
x = 1 (tidak terpenuhi, karena batasan < -4/3)
Jadi, Tidak ada Himpunan penyelesaiannya.
Menyelesaikan Pertidaksamaan Nilai Mutlak
Menyelesaikan pertidaksamaan nilai mutlak caranya hampir sama dengan persamaan nilai mutlak. hanya saja berbeda sedikit pada tanda ketidaksamaannya. Langkah-langkah selanjutnya seperti menyelesaikan pertidaksamaan linear atau kuadrat satu variabel .
Pertidaksamaan mutlak dapat digambarkan sebagai berikut.
Apabila fungsi di dalam nilai mutlak berbentuk ax + b maka pertidaksamaan nilai mutlak dapat diselesaikan seperti berikut.

Lebih jelasnya perhatikan contoh berikut ini.
Contoh
Tentukan himpunan penyelesaian dari Pertidaksamaan nilai mutlak berikut ini.
Jawaban
1. Cara menyelesaikan pertidaksamaan mutlak ini sebagai berikut.
-9 < x+7 < 9
-9 - 7 < x < 9 - 7
-16 < x < 2
Jadi, himpunan penyelesaiannya adalah { x/ -16 < x < 2}
2. Cara menyelesaikan pertidaksamaan mutlak ini dibagi menjadi dua bagian.
(*) 2x - 1 >= 7
2x >= 7 + 1
2x >= 8
x >= 4
(**) 2x - 1 <= -7
2x <= -7 + 1
2x <= -6
x <= -3
Jadi, himpunan penyelesaiannya adalah { x/ x <= -3 atau x >= 4}
3. Kalau dalam bentuk soal ini, langkah menyelesaikan pertidaksamaannya dengan mengkuadratkan kedua ruas.
perhatikan proses berikut ini.
(x + 3)2 <= (2x – 3)2
(x + 3)2 - (2x – 3)2 <= 0
(x + 3 + 2x – 3) - (x + 3 – 2x + 3) <= 0 (ingat: a2 – b2 = (a+b)(a-b))
x (6 - x) <=0
Pembuat nol adalah x = 0 dan x = 6
Mari selidiki menggunakan garis bilangan
Oleh karena batasnya <= 0, maka penyelesaiannya adalah x <=0 atau x >=6.
Jadi, himpunan penyelesaiannya adalah {x/ x <= 0 atau x >= 6}.
Mari selidiki menggunakan garis bilangan
Oleh karena batasnya <= 0, maka penyelesaiannya adalah x <=0 atau x >=6.
Jadi, himpunan penyelesaiannya adalah {x/ x <= 0 atau x >= 6}.
4. Menyelesaikan pertidaksamaan nilai mutlak seperti ini lebih mudah menggunakan cara menjabarkan definisi.
Prinsipnya adalah batasan-batasan pada fungsi nilai mutlaknya.
Perhatikan pada 3x + 1 dan 2x + 4.
Dari batasan batasan itu maka dapat diperoleh batasan-batasan nilai penyelesaian seperti pada garis bilangan di bawah ini.
Dengan garis bilangan tersebut maka pengerjaanya dibagi menjadi 3 bagian daerah penyelesaian.
1. Untuk batasan x >= -1/3 ......(1)
(3x + 1) - (2x + 4) < 10
3x + 1 - 2x- 4 < 10
x- 3 < 10
x < 13 .......(2)
Dari (1) dan (2) diperoleh irisan penyelesaian -1/3 <= x < 13Prinsipnya adalah batasan-batasan pada fungsi nilai mutlaknya.
Perhatikan pada 3x + 1 dan 2x + 4.
Dari batasan batasan itu maka dapat diperoleh batasan-batasan nilai penyelesaian seperti pada garis bilangan di bawah ini.
Dengan garis bilangan tersebut maka pengerjaanya dibagi menjadi 3 bagian daerah penyelesaian.
1. Untuk batasan x >= -1/3 ......(1)
(3x + 1) - (2x + 4) < 10
3x + 1 - 2x- 4 < 10
x- 3 < 10
x < 13 .......(2)
2. Untuk batasan -2<= x < -1/3 ......(1)
-(3x + 1) - (2x + 4) < 10
-3x - 1 - 2x - 4 < 10
-5x - 5 < 10
-5x < 15
-x < 3
x > 3 .......(2)
Dari (1) dan (2) tidak diperoleh irisan penyelesaian atau tidak ada penyelesaian.-(3x + 1) - (2x + 4) < 10
-3x - 1 - 2x - 4 < 10
-5x - 5 < 10
-5x < 15
-x < 3
x > 3 .......(2)
3. Untuk batasan x < -2 ......(1)
-(3x + 1) + (2x + 4) < 10
-3x - 1 + 2x + 4 < 10
-x + 3 < 10
-x < 7
x > -7 .......(2)
Dari (1) dan (2) diperoleh irisan penyelesaian -7 < x < -2. -(3x + 1) + (2x + 4) < 10
-3x - 1 + 2x + 4 < 10
-x + 3 < 10
-x < 7
x > -7 .......(2)
Jadi, himpunan penyelesaiannya adalah {x/ -1/3 <= x < 13 atau -7 < x < -2}.
Perhatikan contoh Pertidaksamaan mutlak lainnya berikut.



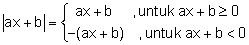








Tidak ada komentar:
Posting Komentar